재귀의 정의
재귀란 자기 자신을 정의하거나 호출하는 것을 말한다.
프로그래밍에서 보통 재귀라고 하면 재귀 함수(recursive call)를 말하며, 함수가 실행 중에 자기 자신을 다시 호출하는 방식의 함수를 의미한다.
재귀 함수의 요건
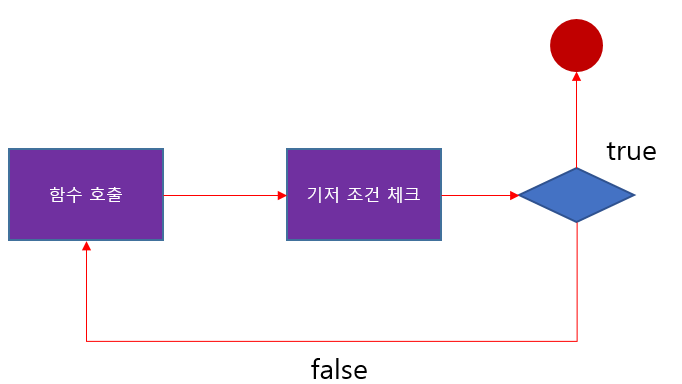
재귀가 자기 자신을 계속 호출한다고 하지만 프로그램이 종료될 수 있도록 설계해야 한다.
따라서 재귀 함수를 구현하는 경우엔 아래 두 가지를 고민해야 한다.
1. 재귀 호출 단계
자기 자신을 호출하는 단계, 보통 호출할 때마다 문제의 크기를 줄여야 한다.
2. 기저 조건
재귀 함수는 언젠가 종료되어야 한다.
특정 조건이 충족되면 더 이상 자기 자신을 호출하지 않고 함수를 종료돼야 한다.
기저 조건이 없으면 무한 재귀로 스택 오버플로우 오류가 발생할 수 있다.
재귀 함수의 설계
재귀 함수로 팩토리얼 로직을 구현해보자.
문제의 정의
N 팩토리얼은 N! 이라고도 하며, N* N-1 * N-2 * ... * 2 * 1로 정의할 수 있다.

재귀적 사고
문제를 정의했으니 이제 문제를 재귀적으로 정의해야한다.
구현하려하는 팩토리얼을 구하는 함수가 있다고 가정한다.
-> Fact(N)은 N!을 반환하는 함수
재귀 함수를 구현할 때에는 다음과 같은 사고방식이 필요하다.
1. 현재 문제는 더 작은 크기의 문제의 해를 이용해 해결한다.
2. 문제의 크기를 계속 줄여나가다가 더 이상 줄일 수 없는 경우에는 직접 해를 구한다.
실제 문제에 적용
N!을 Fact(N)으로 표현했으므로 (N-1)!은 Face(N-1)로 표현할 수 있다.
따라서 Fact(N)은 Fact(N-1) * N으로 표현할 수 있다.
크기가 N인 문제를 크기가 (N-1)인 문제로 표현한것이다. 이 과정이 바로 재귀 단계다.
이것을 확장하면 아래 그림처럼 계속해서 문제의 크기가 줄어들다가 결국 1!을 구해야 하는 상황이 온다.
1!은 더 이상 쪼갤수 없으므로 바로 1을 반환하면 된다. 이것이 바로 기본 단계다.
이제 재귀 함수를 구현하는데 필요한 재귀 호출 단계 및 기저 조건에 대한 설계가 끝났다.
1. 재귀 호출 단계 : Fact(N) = Fact(N-1) * N
2. 기저 조건 : N이 0 또는 1이면 1을 반환
#include <iostream>
using namespace std;
// 팩토리얼을 구하는 재귀 함수
int Fact(int N)
{
if (N == 0 || N == 1) return 1; // 종료 조건 (0! = 1)
return N * Fact(N - 1); // 재귀 호출
}
int main()
{
int num = 5;
cout << num << "! = " << Fact(num) << endl;
return 0;
}
/*
출력 결과:
5! = 120
*/재귀 함수 동작시 메모리의 모습
함수가 호출되면 함수가 동작하는데 필요한 정보들(지역 변수, 매개 변수, 반환 주소 등)이 메모리에 저장된다.
이때 생성되는 메모리 블록을 스택 프레임이라고 한다.
재귀 함수가 반복적으로 호출되는 경우 각 호출마다 새로운 스택 프레임이 생성되어 스택 메모리에 쌓이게 된다.
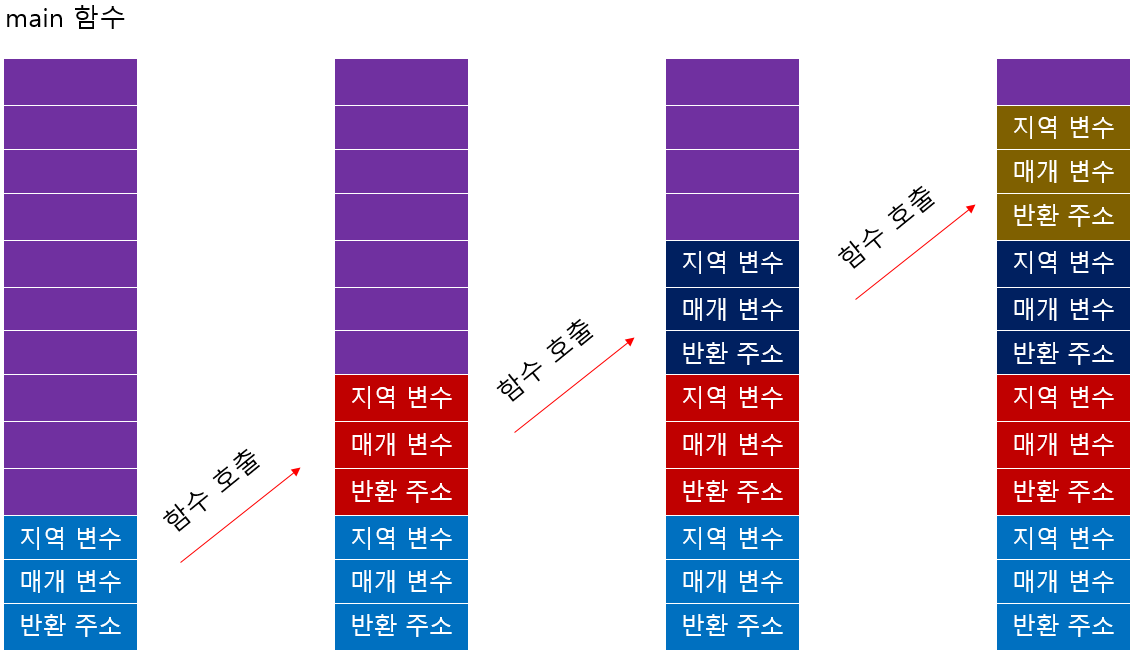
마지막 함수까지 호출이 완료되면 각 함수는 자신을 호출했던 위치로 되돌아가며 종료된다.
이때 반환 주소가 사용되며 이는 자신을 호출한 함수의 코드 위치를 카리킨다.
이 과정을 반복하면서 재귀 호출의 결과가 역방향으로 계산되어 최종 결과가 도출된다.
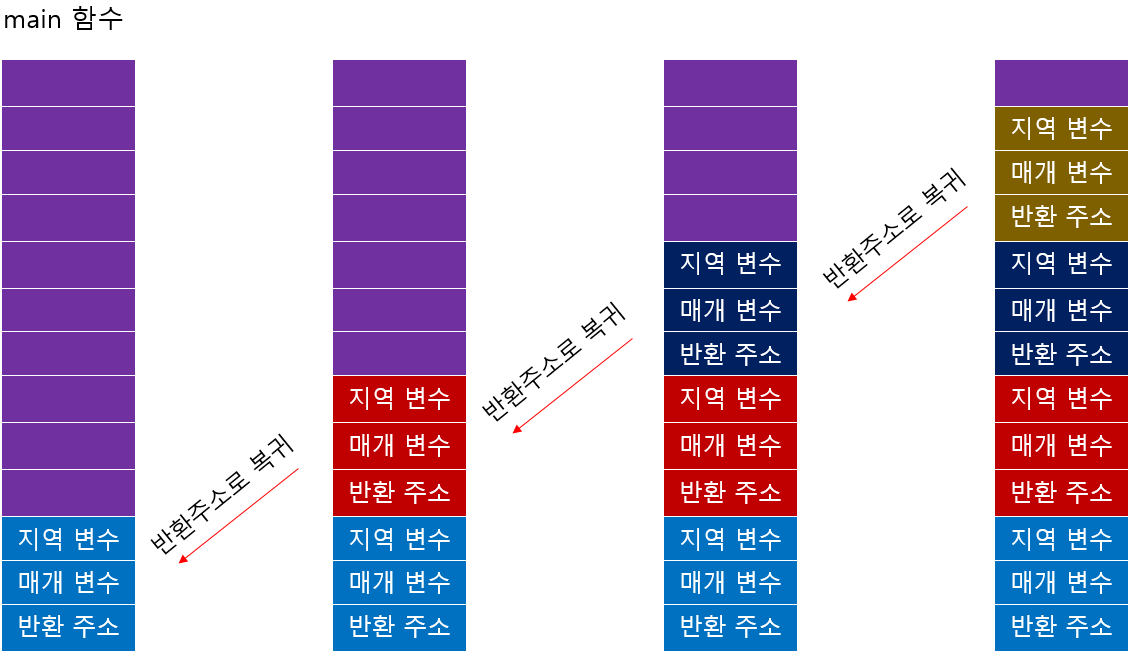
메모리 주의할 점
컴퓨터의 메모리는 한정된 자원이다.
재귀 함수가 호출될 때마다 스택 메모리에 함수의 실행 정보가 저장되므로 호출이 과도하게 누적되면 스택 오버플로우가 발생하여 프로그램이 비정상적으로 종료될 수 있다. 따라서 재귀 함수를 설계할 때에는 다음 사항을 반드시 고려해야 한다.
1. 종료 조건을 명확히 정의해야 한다.
2. 호출 깊이를 적절히 제한하여 메모리 사용을 관리해야 한다.
함수가 호출되어 실행된 후 종료되면 해당 함수의 호출 지점으로 돌아가 중단된 지점 다음부터 실행을 이어간다.
즉 기존 함수는 처음부터 다시 실행되는 것이 아니라 멈췄던 이후 지점부터 실행된다.
#include <iostream>
using namespace std;
// 스택 상태를 출력하며 팩토리얼을 계산하는 재귀 함수
int Fact(int N) {
// 스택에 쌓인 함수 호출을 시각적으로 표현하기 위해 들여쓰기
static int depth = 0;
string indent(depth * 2, ' ');
cout << indent << "Fact(" << N << ") 호출" << endl;
depth++;
if (N == 0) {
depth--;
cout << indent << "Fact(" << N << ") = 1 반환" << endl;
return 1;
}
int result = N * Fact(N - 1);
depth--;
cout << indent << "Fact(" << N << ") = " << result << " 반환" << endl;
return result;
}
int main() {
int num = 5;
cout << num << "! = " << Fact(num) << endl;
return 0;
}
/*
출력 결과:
Fact(5) 호출
Fact(4) 호출
Fact(3) 호출
Fact(2) 호출
Fact(1) 호출
Fact(0) 호출
Fact(0) = 1 반환
Fact(1) = 1 반환
Fact(2) = 2 반환
Fact(3) = 6 반환
Fact(4) = 24 반환
Fact(5) = 120 반환
5! = 120
*/재귀를 사용하는게 효율적인 경우
스택을 사용하는 경우
함수의 호출 과정은 스택 구조를 따른다.
즉 가장 최근에 호출된 함수부터 가장 먼저 종료되는 LIFO(Last In First Out)구조이다.
따라서 명시적인 스택 자료구조 없이도 재귀 호출을 통해 스택 기반 알고리즘을 구현할 수 있다.
가장 대표적인 예는 깊이 우선 탐색 이다.
1. 현재 노드를 방문 처리한다.
2. 인접한 노드 중 방문하지 않는 노드를 재귀적으로 방문한다.
3. 더 이상 방문할 노드가 없으면 이전 노드로 되돌아간다.

#include <iostream>
#include <vector>
using namespace std;
// 그래프를 인접 리스트로 표현
vector<int> graph[9];
bool visited[9];
// DFS 함수 정의
void DFS(int node) {
visited[node] = true;
cout << node << ' ';
for (int i = 0; i < graph[node].size(); i++) {
int next = graph[node][i];
if (!visited[next]) {
DFS(next);
}
}
}
int main() {
// 그래프 초기화
graph[1] = {2, 3, 8};
graph[2] = {1, 7};
graph[3] = {1, 4, 5};
graph[4] = {3, 5};
graph[5] = {3, 4};
graph[6] = {7};
graph[7] = {2, 6, 8};
graph[8] = {1, 7};
// DFS 실행
DFS(1);
return 0;
}
/*
출력 결과:
1 2 7 6 8 3 4 5
*/분할 정복 알고리즘으로 해결하는 경우
분할 정복 알고리즘은 문제를 작게 나누고 동일한 방법으로 해결한 뒤 결과를 결합하여 전체 문제를 푸는 방식이다.
1. 분할 : 문제를 더 작은 부분 문제로 나눈다.
2. 정복 : 각 부분 문제를 재귀적으로 해결한다.
3. 결합 : 부분 문제의 해를 합쳐서 원래 문제를 해결한다.
이 절차는 재귀적으로 문제를 해결하는 과정과 유사하다.
대표적인 예는 병합 정렬이 있다.
1. 분할 : 현재 배열을 반으로 나눈다.
2. 정복 : 각 부분 배열을 재귀적으로 병합 정렬한다.
3. 결합 : 정렬된 부분 배열들을 병합하여 하나의 정렬된 배열로 만든다.
위 방식으로 배열을 더 이상 쪼갤 수 없을 때까지 분할하고 각 부분을 정렬한 뒤 병합함으로써 전체 배열을 정렬한다.
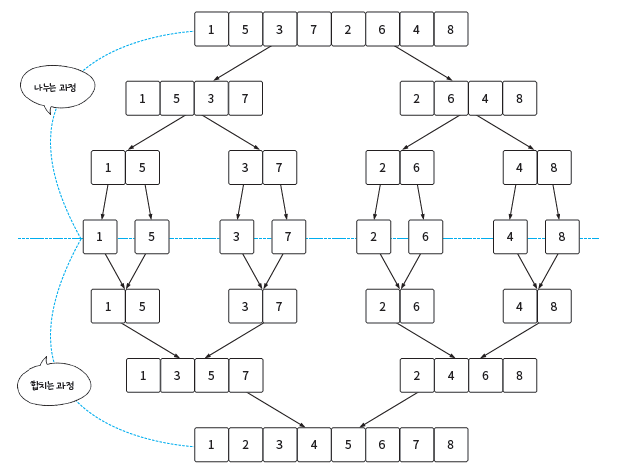
재귀 사용시 조심해야 하는 부분
위에서 말했듯이 재귀 함수를 사용할 때는 호출될 때마다 점점 더 많은 메모리를 사용하게 되므로 함수가 과도하게 호출되지 않도록 주의해야한다.
직관적인 예시로 피보나치 수열을 재귀적으로 계산해보자.
피보나치 수열은 첫 번째와 두 번째 수가 각 1이며 그 이후의 수는 앞의 두 수를 더한 값으로 정의된다.
1. 기저 조건
피보나치수열의 맨 앞 두 수는 1이다. 이것은 더 이상 쪼갤 수 있는 문제가 아니므로 직접 반환한다.
2. 재귀 호출 단계
N 번째 피보나치 수를 구하는 함수 fibo(N)이 있다고 가정하고 N 번째 피보나치 수는 N-1 번째와 N-2 번째 피보나치 수의 합이다.
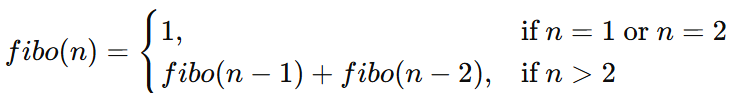
큰 문제가 없어 보이지만 하나의 함수가 두 개의 함수를 호출하는 방식이므로 호출되는 함수의 총 개수가 굉장히 빠르게 증가한다.
그리고 중복되는 함수 호출이 많다.

중복되는 함수 호출을 줄이는 방법은 한 번 계산한 결과를 저장해두고 이후에는 다시 계산을 하지 않는 것이다.
이러한 기법을 메모이제이션 이라고 한다.
메모이제이션
피보나치 수열을 구하는 재귀 함수에 메모이제이션을 적용해보자.
1. fibo(N)이 이미 계산된 값인지 확인한다.
2. 이미 계산된 값이면 추가적으로 함수를 호출하지 않고 저장된 값을 바로 반환한다.
3. 계산이 안된 값이면 fibo(N-1) + fibo(N-2)를 계산한 뒤 저장하고 그 값을 반환한다.
메모이제이션을 적용하면 호출 과정이 전과 달리 중복 연산이 많이 줄어든다.

// 메모이제이션을 사용하지 않은 단순 재귀 피보나치 수열 계산
#include <iostream>
using namespace std;
// 피보나치 수열을 재귀적으로 계산하는 함수
int fibo(int n) {
if (n == 1 || n == 2) return 1;
return fibo(n - 1) + fibo(n - 2);
}
int main() {
int n = 10;
cout << "fibo(" << n << ") = " << fibo(n) << endl;
return 0;
}
/*
출력 결과:
fibo(10) = 55
*/// 메모이제이션을 사용한 피보나치 수열 계산
#include <iostream>
#include <vector>
using namespace std;
// 메모이제이션을 위한 배열 초기화
vector<int> memo(1000, -1);
// 피보나치 수열을 메모이제이션을 활용하여 재귀적으로 계산하는 함수
int fibo(int n) {
if (n == 1 || n == 2) return 1;
if (memo[n] != -1) return memo[n];
memo[n] = fibo(n - 1) + fibo(n - 2);
return memo[n];
}
int main() {
int n = 10;
cout << "fibo(" << n << ") = " << fibo(n) << endl;
return 0;
}
/*
출력 결과:
fibo(10) = 55
*/메모이제이션을 사용한 코드를 디버깅하면서 확인해보니
1. fibo(n - 1)을 우선 n = 2가 될 때 까지 파고들고
2. n = 2가 되면 fibo(2) = 1을 반환하고
3. 호출 지점(n = 3)으로 돌아가서 fibo(1)을 호출하고
4. fibo(1) = 1을 반환 후 다시 호출지점(n = 3)으로 돌아가서
5. memo[3] = 2를 반환하고 또 호출 지점(n=4에서 memo[4] = fibo(3) + fibo(2)의 fibo(3) 부분)으로 돌아가서
6. fibo(2) = 1을 더한 값을 memo[4] = 3을 반환하고
7. 이후 memo[5]부터는 fibo(n -2)를 호출하지만 미리 저장된 memo[n - 2] 값을 반환하여 더한 값이 저장되는 구조였다.
재귀의 예시(지수 연산)
X의 N 승을 반환하는 함수를 재귀로 구현해보자. (N은 음이 아닌 정수)
1. 기저 조건
X의 0승은 1이다.
2. 재귀 호출 단계
X의 N승을 계산하는 함수 pow(X, N)이 이미 있다고 가정.
-> pow(X, N) = pow(X, N-1) * X

정리
재귀의 두 가지 핵심 단계.
1. 기저 조건
더 이상 분할되지 않는 종료 조건
2. 재귀 단계
가지 가신을 호출하여 문제를 해결하는 과정
재귀와 반복문의 장단점
| 특성 | 재귀 함수 | 우위 | 반복문 |
| 정의 | 함수가 자기 자신을 호출하여 작업을 수행. | for, while 등의 제어 구조를 사용하여 반복 수행. | |
| 메모리 사용 | 각 함수 호출 시 스택 메모리를 사용하며 호출이 깊어지면 스택 오버플로우가 발생할 수 있음. | < | 스택 메모리를 사용하지 않으며 일반적으로 빠른 실행 속도를 가짐. |
| 실행 속도 | 함수 호출과 복귀를 위한 컨텍스트 스위칭으로 인해 반복문보다 느릴 수 있음. | < | 함수 호출 없이 반복을 수행하므로 일반적으로 빠른 실행 속도를 가짐. |
| 가독성 | 코드가 간결하고 특히 알고리즘이 재귀적으로 표현되기에 자연스러운 경우 가독성이 높음. | > | 코드 길이가 길어질 수 있으며 많은 변수를 사용하게 되어 가독성이 떨어질 수 있음. |
| 변수 사용 | 상태를 유지하기 위해 추가적인 변수를 사용하지 않아도 되어 코드가 간결해짐. | > | 상태 유지를 위해 여러 변수를 사용해야 할 수 있어 코드가 복잡해짐. |
| 무한 반복 시 | 종료 조건을 잘못 설정하면 스택 오버플로우가 발생할 수 있음. | = | 종료 조건을 잘못 설정하면 CPU를 계속 사용하게 되어 시스템에 부하를 줄 수 있음. |
'코딩테스트 공부' 카테고리의 다른 글
| 효율적인 코드 구현하기(벡터vs덱, 정렬이 필요없는데 정렬하는 경우, 특정 원소 찾기, 문자열 결합하기, auto& vs auto) (0) | 2025.09.29 |
|---|---|
| STL 사용하기(반복자, 컨테이너(vector, set, map), 알고리즘(sort, find, count, unique)) (0) | 2025.09.29 |
| 입력값 처리(숫자 반올림, 올림, 내림, 문자열 스트림, 진법 변환) (0) | 2025.09.29 |
| 자주 하는 실수(단락 평가, off by one, 0으로 나누기, 중간 값의 오버플로) (0) | 2025.09.26 |
| 문자열 메서드(find, append, replace, substr 등) (0) | 2025.09.26 |
